Regel 3 – Lagen om hur variation påverkar flöden (Kingmans ekvation)

Lagen om hur variation påverkar flöden (Kingmans ekvation)

I alla flöden finns alltid en viss naturligt variation. En regnig dag flyter det mer vatten i en bäck än dagar det är klart väder. På morgonen när människor ska till jobbet är det fler bilar i trafiken än strax innan lunch.

Som vi visat tidigare i detta kapitel finns det ett samband mellan variationen i flödet och dess flödeseffektivtet samt resurseffektivitet.

Variation kan minska flödeseffektivtiten och skapa köer

När det är många ”flödesenheter” i omlopp är det inte säkert att resurserna räcker till. Vägen rymmer inte alla bilar, vårdcentralen hinner inte ta emot alla patienter. Då bildas det köer vilket minskar flödeseffektiviteten.

Variation kan minska resurseffektiviteten och skapa slöseri

Variationen slår såklart även åt andra hållet. Strax innan lunch är det mindre bilar på vägen, vilket leder till vägen inte används så “effektivt” som den skulle kunna. Resurseffektiviteten blir lägre!

Om vi återvänder till den modell vi presenterade i början av kapitlet kan sambandet visas på följande sätt:

Variationen sätter alltså ett övre tak för hur effektivt ett flöde kan vara. Större variation gör taket ”större”.

Kingmans ekvation

Kingmans ekvation är ett sätt att beskriva detta samband matematiskt. Formeln ser ut på följande sätt:

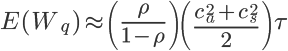E( Wq ) är den genomsnittliga kötiden (alltså genomloppstiden som är ett mått på flödeseffektiviteten).p  är hur mycket en resurs utnyttjas, dvs. ett mått på resurseffektiviteten. I formeln uttrycks detta som ett decimaltal mellan 0 och 1 (där 1 är detsamma som 100% resurseffektivitet). Ca2 + Cs2 är den genomsnittliga variationskoefficenten för ankomstid (ex. den procentuella variationen i inflödet av patienter till en mottagning) och processtid (ex. den procentuella variationen av en tidsåtgången för en behandling). T  är den genomsnittliga processtid (dvs. cykeltiden). Läs mer: http://en.wikipedia.org/wiki/Kingman’s_formula

Maximal flödeseffektivitet eller maximal resurseffektivitet?

Kingsmans ekvation tvingar oss alltså att välja mellan resurseffektivitet och resurseffektivitet. Därför räcker det inte med att bara säga att vi vill öka ett flödes effektivitet. Vi måste också bestämma oss vilken typ av effektivitet vi vill öka!

Vill vi satsa på att öka resurseffektiviteten (som i A) eller vill vi istället prioritera att öka flödeseffektiviteten (som i B eller C)?

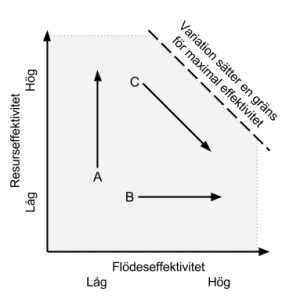
Hur mycket vi än anstränger oss kommer vi aldrig att kunna uppnå båda!

Slutsatser

De slutsatser vi kan dra från kingsmans formel är följande:

• För att säkerställa hög resurseffektivitet måste vi säkerställa att vi alltid kan utnyttja våra resurser fullt ut. Därför behöver vi en buffert av ”flödesenheter”, dvs en kö med patienter!
• För att nå en resurseffektivitet på 100% krävs en oändlig kö (dvs. en obefintlig flödeseffektivitet, detta visas i formeln genom att p = 1 ger division med noll!)
• Ökad variation (både i ankomsttid och processtid) ökar genomloppstiden (dvs. lägre flödeseffektivitet).
• Ökad processtid ökar genomloppstiden (dvs. lägre flödeseffektivitet).

Ok, men hur gör vi då för att öka flödeseffektiviteten?